慶應義塾理工学部 物理情報工学科3年必修 制御工学 13年度講師 足立修一教科書 足立修一:MATLABによる制御工学 東京電機慶應義塾理工学部 物理情報工学科3年必修 制御工学 13年度講師 足立修一教科書 足立修一:MATLABによる制御工学 東京電機図 4 ボード線図の例 図 5 ゲイン線図における折れ線近似 図 6 ボード線図上の直列接続の計算(ゲ イン線図) (注3) ナイキスト線図の場合は負の角周波数も考える 計測と制御 第42巻 第4号 03年4月 号 69 安定性解析に向いており,33で 触れることにする
ボード線図を書こう Keio Robotics Association
ボード線図 折れ線近似
ボード線図 折れ線近似-物理学 ボード線図 ボード線図を折れ線近似で書く時、G(s)=Ts1(Tは時定数)のTがマイナスになってしまう問題があります。 例えばT=10ではゲイン曲線は0dB(ωボード線図(ボードせんず、英 Bode plot )は、線形時不変系における伝達関数の周波数特性を表した図であり、通常はゲイン線図と位相線図の組合せで使われる。 1930年代にヘンドリック・W・ボードによって考案された。 ボード図またはボーデ線図とも。



周波数応答 またはゲインと位相データのボード線図 Matlab Bode Mathworks 日本
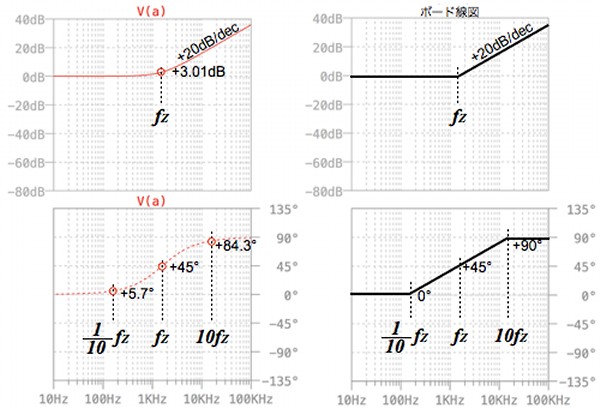
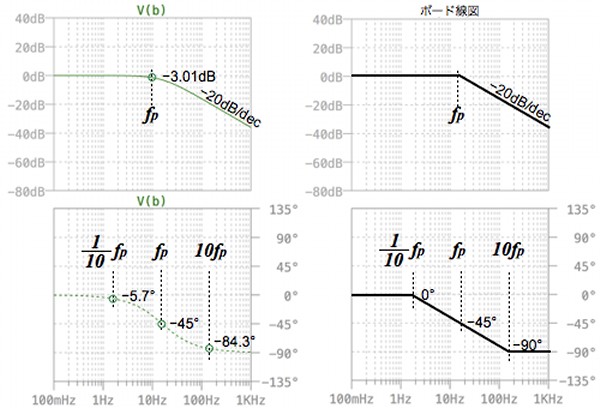
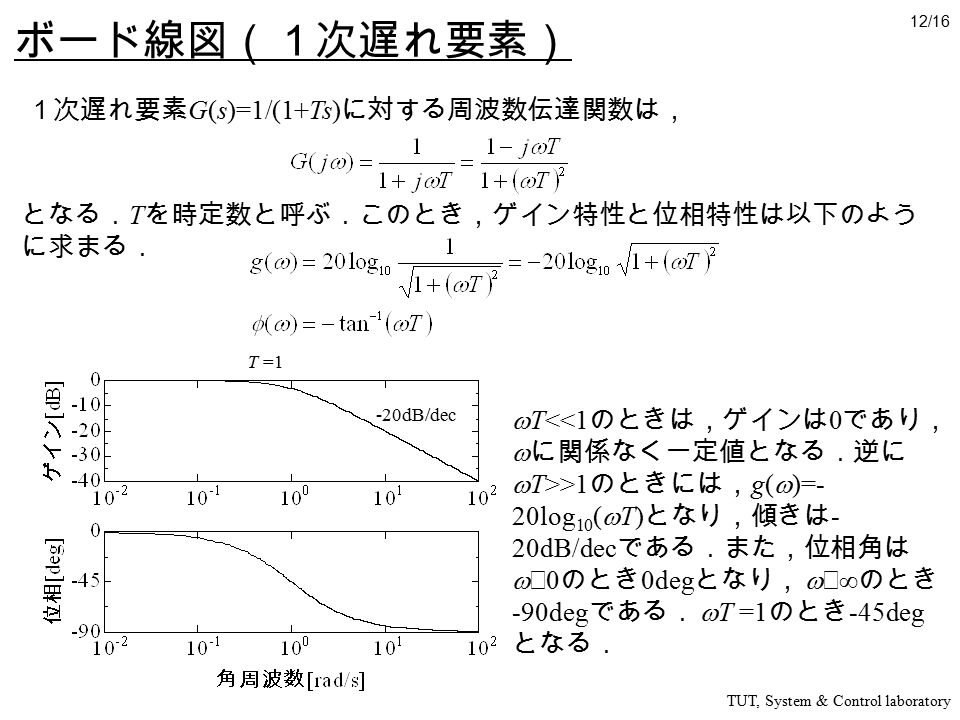
伝達関数 に含まれる1次進み要素 について、漸近線近似を用いてボード線図を求めていきます。 1次進み要素のゲイン線図は 2つの漸近線 を用いて近似することが出来ます。 今回の1次進み要素 の場合は、周波数 が 5rad/sec までゲイン 0dB の漸近線で表し、そのあと傾き dB/decade の漸近線を用いて表します。 1次進み要素の位相線図は 3つの漸近線 を用いて近似折れ線近似 (ゲイン)0 dB と– dB/dec の2 本の直線 (位相) T 02 ω≤ 0o T 5 ω≥ −90o で で (b)位相線図 位相゜ 図5 7 1 次系のボード線図 (a)ゲイン線図 ゲイン dB −40 − 0 10−2 10−1 100 101 102 ωT −180 −90 90 0 10−2 10−1 100 101 102 ωT 折点周波数 T 1 ω= 22ボード線図で、s>jwと置き換えて、G(jw)=1jwT として、Gの絶対値、位相を見てるのですよね。 ここで、T=10のときは、1j10w で、ゲインはT=10と同じで、位相の進み遅れが変わる(位相の絶対値は同じ)になるかと。
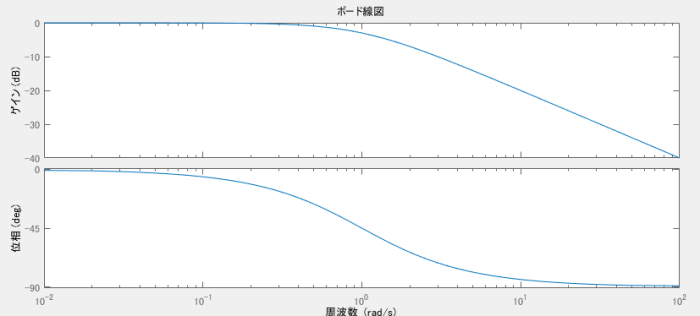
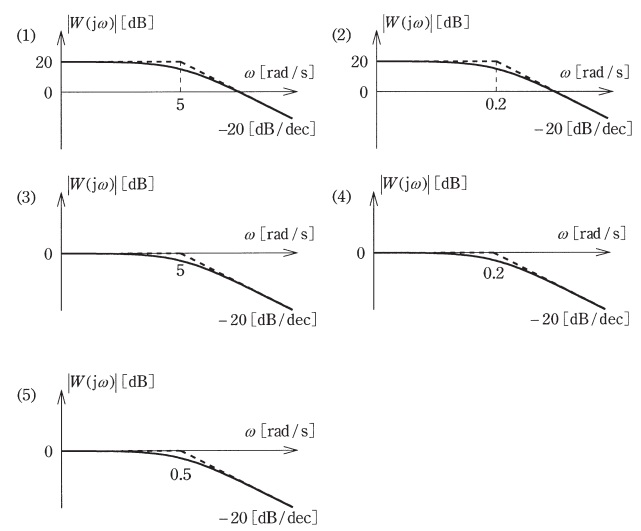
慶應義塾理工学部 物理情報工学科3年必修 制御工学 13年度講師 足立修一教科書 足立修一:MATLABによる制御工学 東京電機問17 図は,ある周波数伝達関数$ W(j \omega) $のボード線図の一部であり,折れ線近似でゲイン特性を示している。 次の(a)及び(b)の問に答えよ。 (a)図のゲイン特性を示す周波数伝達関数として,最も適切なものを次の(1)~(5)のうちから一つ選べ。ボード線図の作図方法 (折れ線近似)につきまして質問いたします。 古典制御工学初学者です。 (110s)/ (12s) という要素のボード線図を折れ線近似にて作図したいのですが、ゲイン線図が添付図のようにはならずに、10 (dB)で一定となってしまいます。 (画像が見えない場合のために作図に使用したwebサイトのurlを添付いたします。 http//iso22jp/bode_drawer/ ) そもそも
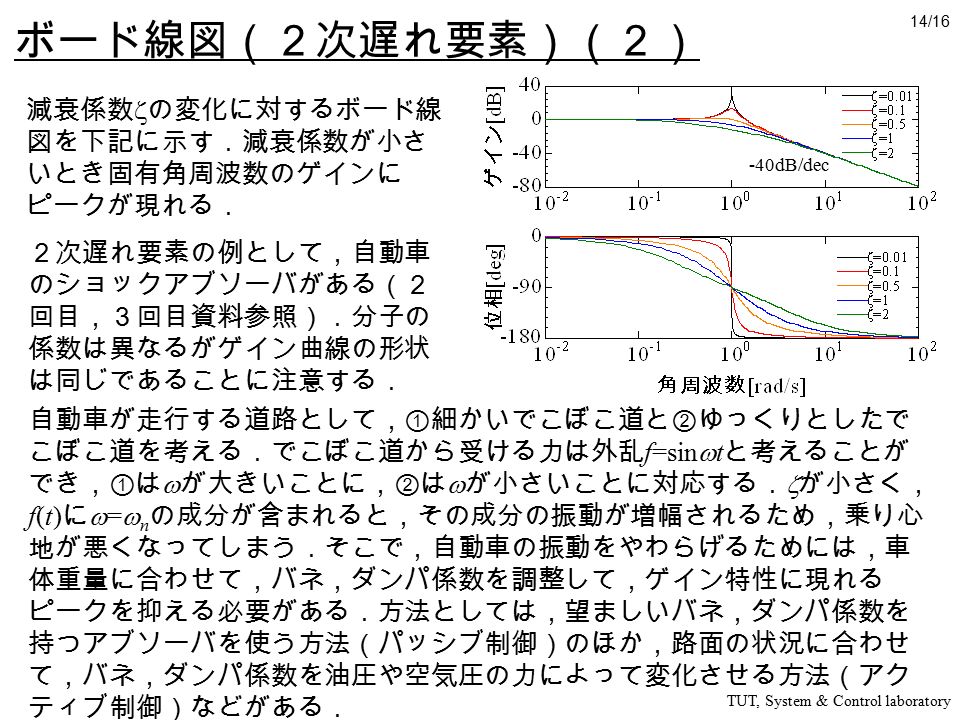
ボード線図 二次のシステム •低周波領域ωω/ωn) • 0dBの水平線 •交点(折点周波数) •ω/ωn=1→固有角周波数ω=ωn •減衰比ζで共振点でのピーク値が変わる • 折れ線での近似値0dB • 減衰比ζが小さいと,ピークが大きくなり,近似からの乖離大 log 1ボード線図では対数の底はe ではなく10 係数に がついている 習慣的に使われている単位(dB)にあわせた dB(デシベル)はB(ベル)の1 10 dL と同じd,1 10 の意味 cm のc は 1 100 ,mm のm(ミリ)は 1000 浅井 徹 (名古屋大学) ボード線図のしくみボード線図のこの性質のおかげで,標準的な周波数伝達関数のゲイン特性を近似的に 描くことが容易になる(この資料の232 節). ゲインの計算については,次項を参照のこと.


制御工学のボード線図についての問題です 次の伝達関数の周波数応答をボ Yahoo 知恵袋



ボード線図に関する問題です Okwave
ブロック線図からボード線図をプロットするにはどうすれば良いですか? Learn more about ボード線図, 線形化, simulink, モデル Simulinkのボード線図(ゲイン線図, 位相線図ともに折れ 線近似) は, Fig 1319(a) で与えられる P(s) のボード線図を, 折 れ線近似により, Fig 1319(a) に記入しなさい 2 C1(s) のボード線図は, Fig 1319(b) で与えられる 開ループ特性 L1(s) = P(s)C1(s) のボード線図を, 折れ線近似フィードバック制御入門 5 章演習問題5 1 5 章演習問題5 つぎの伝達関数のボード線図の概形を描け ただし, ゲイン線図は折れ線近似でよい (a) 10s 1 s 10 (b) s 10 10s 1 (c) 1 s−1 解答 (a) 周波数伝達関数は, G(jω) = 1 j10ω 10 jω (1) である


ボード線図
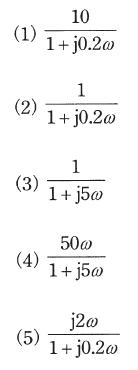


H27 機械 問17 電験三種 これでok
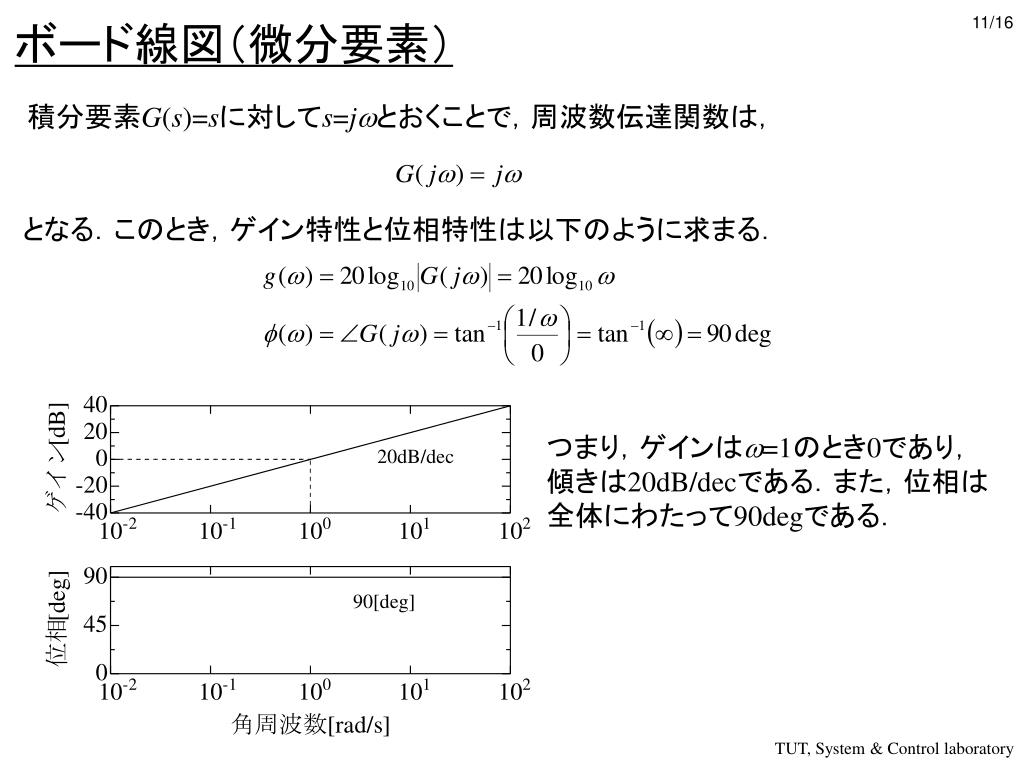
もしも,ブロック線図を作るとすると図の通りとなる. 16 式(15)において,a=10,C0 =y(0)=5とすればy(t)=5e−10t となる. 21 問1現在の出力,現在の入力, 問2現在の出力,過去の入力,微分方程式 22 図28の運動方程式は以下で表される. M¨y(t)Dy˙(t)=f(t) (A1)ボード線図 比例・微分・積分 1次遅れ,ムダ時間 パデ近似の導出 pade関数の作成 制御の安定性 ブロック線図 フィードバック 2次遅れ系 ステップ応答法 周波数応答法 ナイキスト線図 安定性の判別 判別の仕組み 安定余裕の評価 評価の例題次の問題が分からないので教えて欲しいです。 R=kΩ C=10μFとする。 Viを入力、Voを出力とする系のボード線図を描け。(折れ線近似したもので可) そしてViに印加される正弦波の角周波数が十分大きいとき、こ


宮崎技術研究所 自動制御講座 3 2 2 周波数応答による評価



Ppt 第 7 週目 周波数伝達関数とボード線図 Powerpoint Presentation Id
つぎの伝達関数のボード線図の概形を描け ただし, ゲイン線図は折れ線近似でよい (a) 10s1 s 10 (b) s10 10s1 (c) 1 s − 1 解答 (a) 周波数伝達関数は, G(jω)= 1j10ω 10jω (1) である (解法1) ゲインと位相はそれぞれつぎのように表される G(jω) = 1j10ω 10jω = 1100ω2 100ω2 (2) ∠G(jω)=ニコルス線図 0100 80 60 40 0deg dB 1jωT 0 10 001 01 1 10 100 ω dB9045 0 001 01 1 10 100 Φdeg ω ボード線図 ナイキスト線図 ニコルス線図図2 (b)のボード線図 19年度制御工学II 前期第4回レポート(模範解答) 2 問題2 次の伝達関数のゲイン線図を折れ線近似で



ボード線図を書こう Keio Robotics Association



ボード線図を書こう Keio Robotics Association
ボード線図のゲイン特性の描き方 () 鹿児島大学・工・電気電子 田中哲郎 41 ボード線図のゲイン特性の描き方 実際の制御系の周波数応答とゲイン 各要素のゲイン特性(分子) ゲイン特性(分子)の折れ線近似 ゲイン特性(分母)の折れ線近似電験2種ではボード線図でこの曲線部分を正確に描く事は困難なので、問題文で 「折れ線近似で書け」 という条件がついていることがほとんどです。 折れ線近似 で表すと下図のようになります。 なんとなく分かりますよね!!!(うまく言葉に出来ないので講義12 ボード線図の特性と周波数伝達関数 ポイント ・ボード線図の合成について理解しよう. ・2次遅れ系のボード線図の特徴を理解しよう Text 佐藤,平元,平田:はじめての制御工学,講談社 y(t) u(t) 出力 入力 時間関数で書いたもの



制御工学 Scilabを使ってボード線図を描いてみた Qiita


ボード線図を用いたゲインと位相の解析 Cq出版社 オンライン サポート サイト Cq Connect
ボード線図 二次のシステム •低周波領域ωω/ωn) • 0dBの水平線 •交点(折点周波数) •ω/ωn=1→固有角周波数ω=ωn •減衰比ζで共振点でのピーク値が変わる • 折れ線での近似値0dB • 減衰比ζが小さいと,ピークが大きくなり,近似からの乖離大 log 1伝達関数と各要素のボード線図 前々回 からの続きとして、伝達関数 が与えられた場合のボード線図を求めていきます。 実際に伝達関数からボード線図を漸近線近似で書いてみよう ロボットや工作機械などのシステムの伝達関数が与えられた場合に、ボード線図を書く方法を紹介します。 前回までの記事で この伝達関数 を と変換し、この変換した伝達関数 を53 下図はボード線図の折れ線近似ゲインである.最小位相系であるとして,伝達関数を求め よ.dB/dec 40 40dB/dec 10 dB/dec 40dB/dec Ans 50(02s 1) s(2s 1)((1/16)s 1) log G(j ω) dB ω1 5 16 ω→ 54 下図の系について (a) 減衰率ςおよび固有周波数ωnを求めよ



ボード線図 電験3種 理論 最速合格
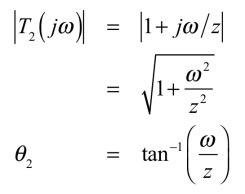


ボード線図を用いたゲインと位相の解析 Cq出版社 オンライン サポート サイト Cq Connect


第 7 週目 周波数伝達関数とボード線図 周波数伝達関数 ボード線図 Tut System Control Laboratory 1 Ppt Download



ボード線図 電験3種 理論 最速合格



自動制御 演習問題 Cupuasu クプアス


ボード線図を用いたゲインと位相の解析 Cq出版社 オンライン サポート サイト Cq Connect



自動制御 演習問題 Cupuasu クプアス


電験三種 過去問解説 機械 問17 平成27年度 電験王3


H27 機械 解説17 Yaku Tik 電験三種まとめました



ボード線図を書こう Keio Robotics Association


Ppt 第 7 週目 周波数伝達関数とボード線図 Powerpoint Presentation Id
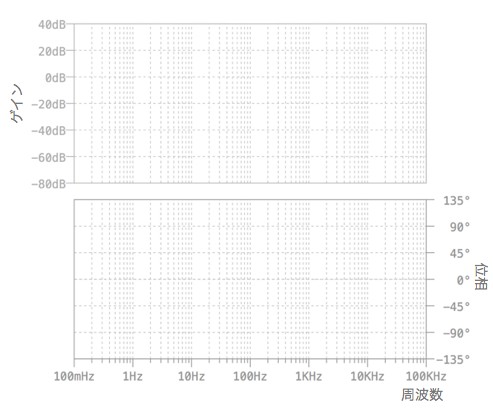


ボード線図を用いたゲインと位相の解析 Cq出版社 オンライン サポート サイト Cq Connect


ボード線図



ボード線図 Wikipedia


制御工学の質問です 次の伝達関数を基本要素に分解し ゲイン線図 Yahoo 知恵袋


ボード線図



制御システム 制御系



ボード線図 電験3種 理論 最速合格



周波数応答 またはゲインと位相データのボード線図 Matlab Bode Mathworks 日本


宮崎技術研究所 自動制御講座 3 2 2 周波数応答による評価
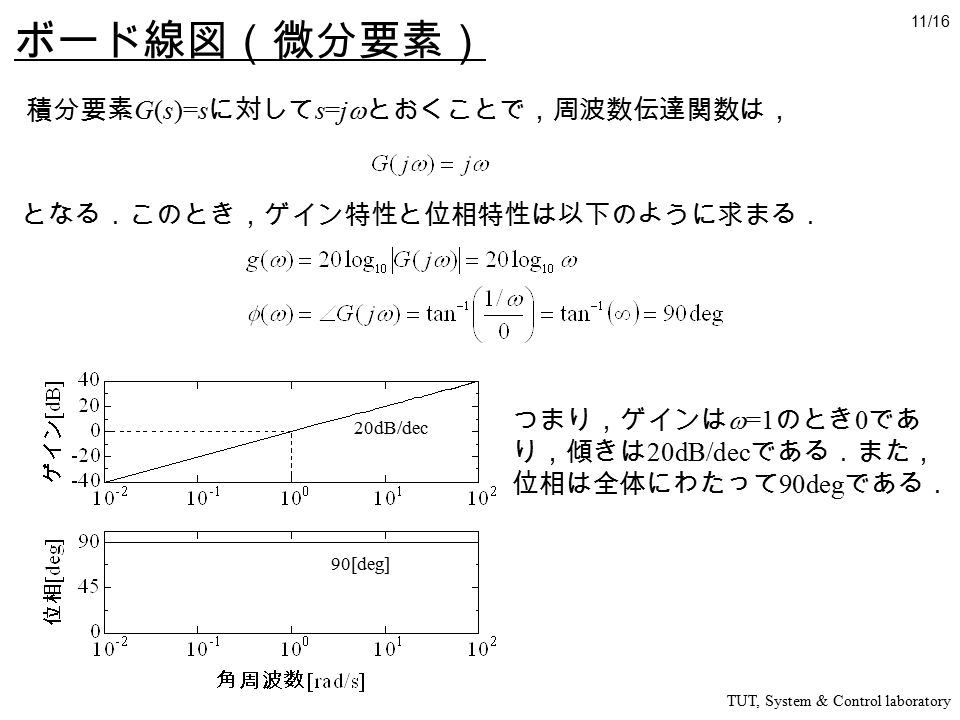


第 7 週目 周波数伝達関数とボード線図 周波数伝達関数 ボード線図 Tut System Control Laboratory 1 Ppt Download
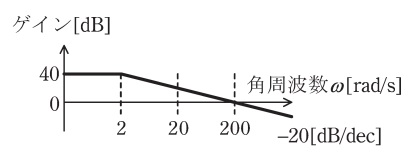


機械 自動制御 R2 問17 ブロック線図と周波数伝達関数及びボード線図に関する計算問題 電験王3



制御工学の周波数応答 1次遅れのボード線図について Okwave


Scilab フィードバック制御入門 周波数応答 ボード線図
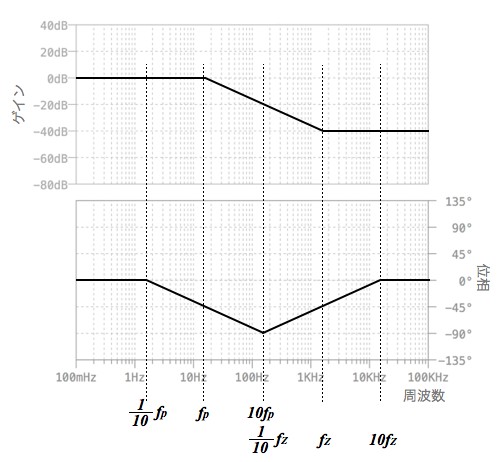


ボード線図を用いたゲインと位相の解析 Cq出版社 オンライン サポート サイト Cq Connect
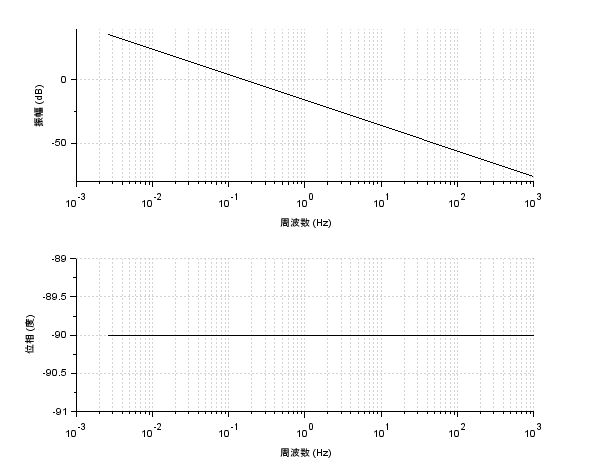


制御工学 Scilabを使ってボード線図を描いてみた Qiita


ボード線図


ボード線図の書き方 2次遅れ系


ボード線図の作図方法 折れ線近似 につきまして質問いたします 古典制御工 Yahoo 知恵袋
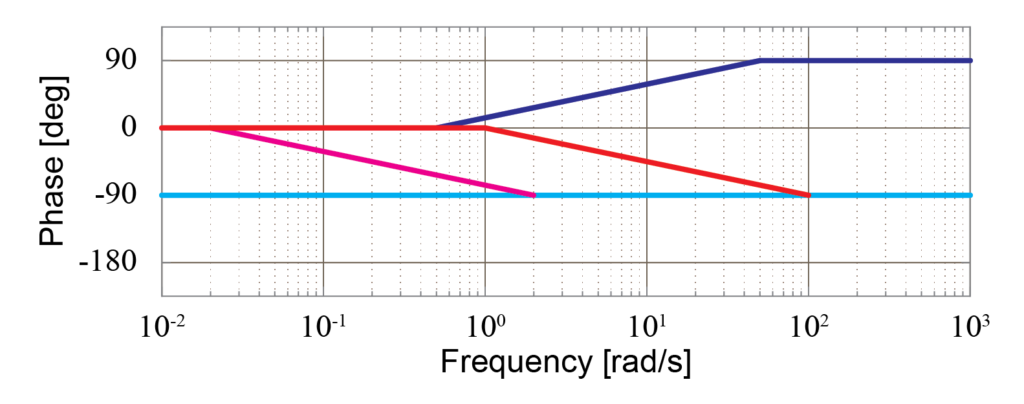


実際に伝達関数からボード線図を漸近線近似で書いてみよう その3 Tajima Robotics
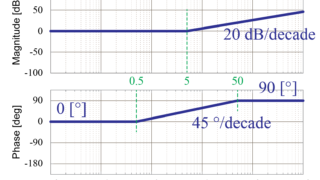


実際に伝達関数からボード線図を漸近線近似で書いてみよう その3 Tajima Robotics


ボード線図の書き方 2次遅れ系



ボード線図 位相余裕 ゲイン余裕 Okwave



制御システム 制御系
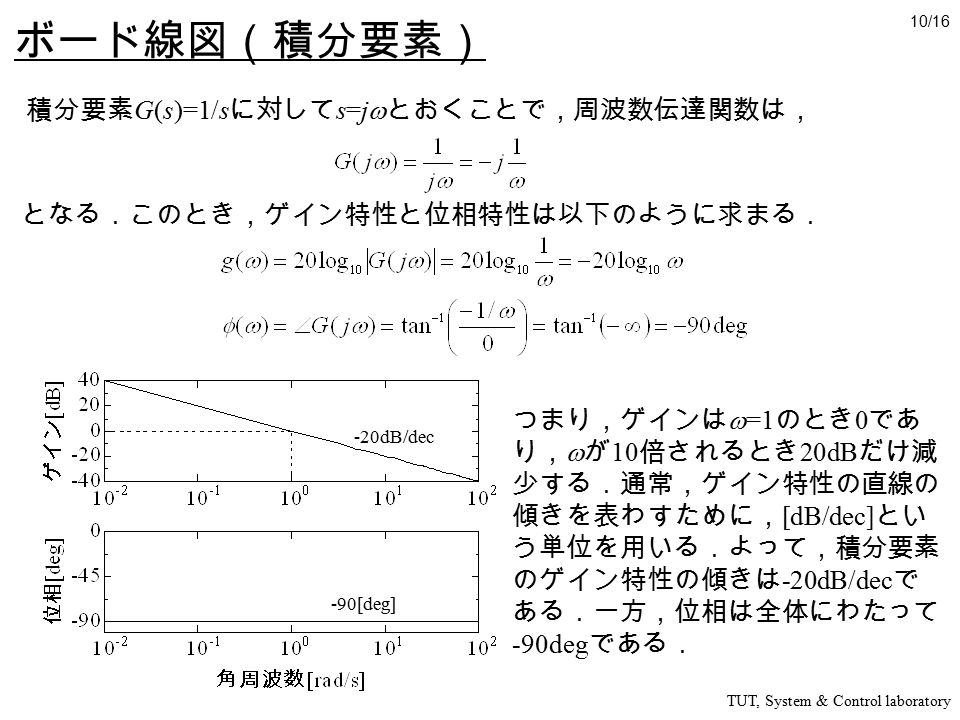


第 7 週目 周波数伝達関数とボード線図 周波数伝達関数 ボード線図 Tut System Control Laboratory 1 Ppt Download
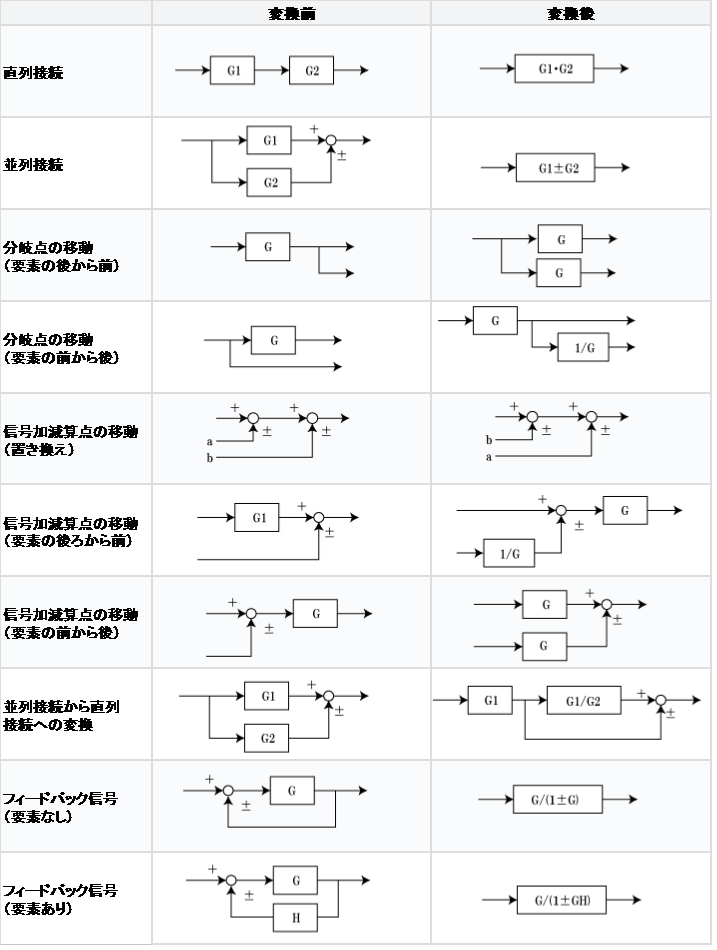


ブロック線図と伝達関数 基礎からわかる電気技術者の知識と資格



制御システム 制御系
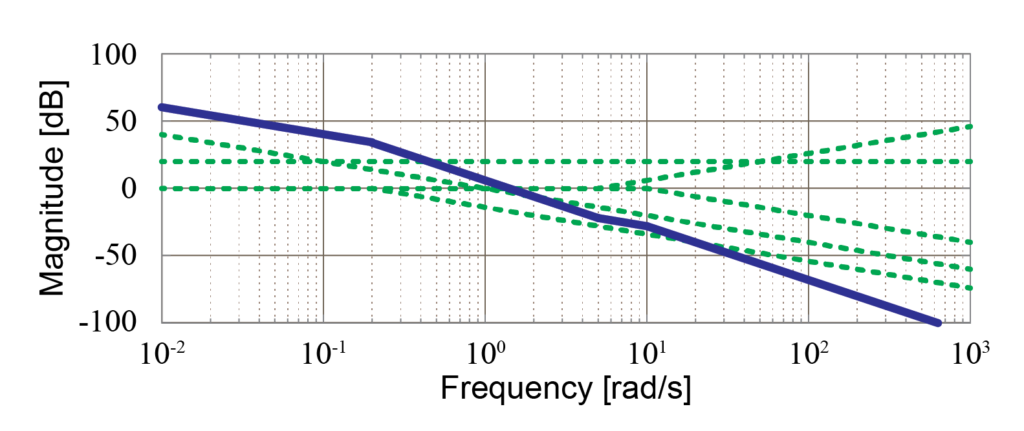


実際に伝達関数からボード線図を漸近線近似で書いてみよう その3 Tajima Robotics



ボード線図 Wikiwand
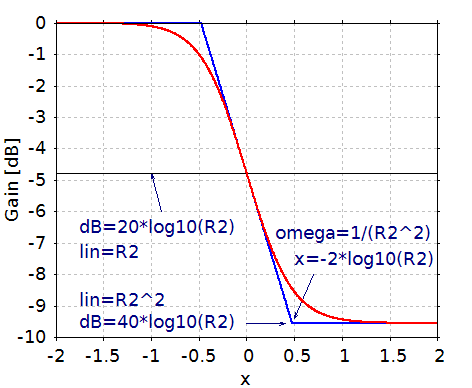


3 3 V ノイズジェネレータ 5 シンセ アンプラグド


制御工学の課題です 1 10s 1 のボード線図の書 Yahoo 知恵袋


ボード線図



慶應大学講義 制御工学同演習第六回 ボード線図の描き方 Youtube



ボード線図 電験3種 理論 最速合格


ボード線図から伝達関数を推定する方法を教えてください 下図の様なボード線 Yahoo 知恵袋
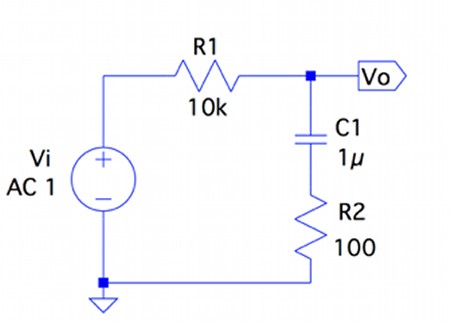


ボード線図を用いたゲインと位相の解析 Cq出版社 オンライン サポート サイト Cq Connect


以下の伝達関数のボード線図を折れ線近似で描く G S 10s Yahoo 知恵袋
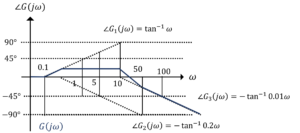


自動制御 演習問題 Cupuasu クプアス



制御工学 古典制御 に関する質問です Okwave



ボード線図 Wikipedia
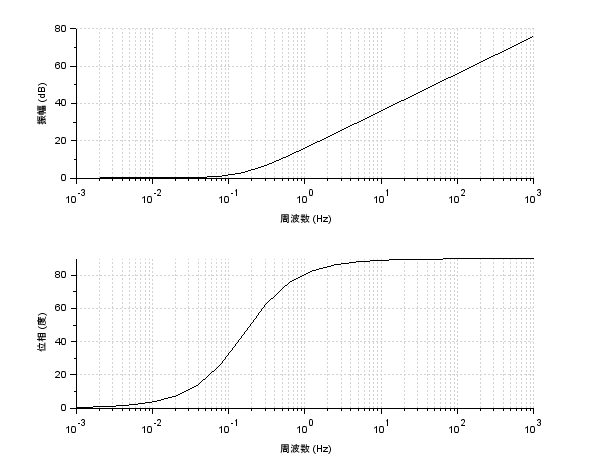


制御工学 Scilabを使ってボード線図を描いてみた Qiita



ボード線図 電験3種 理論 最速合格


ボード線図 Wikiwand



ボード線図 電験3種 理論 最速合格
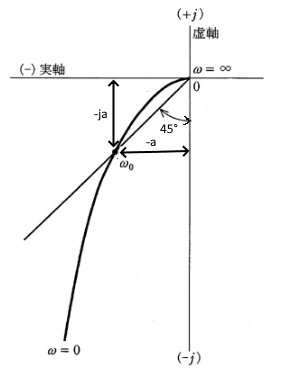


ブロック線図と伝達関数 基礎からわかる電気技術者の知識と資格


G S S 10 S 5のボード線図を折線近似で求めて描いてくれませんか Yahoo 知恵袋


ボード線図の書き方 2次遅れ系
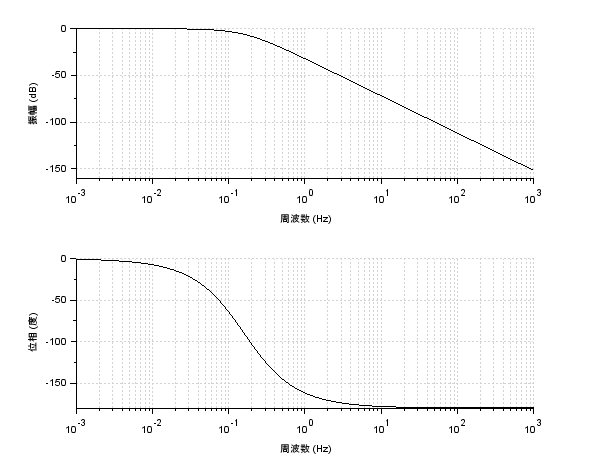


制御工学 Scilabを使ってボード線図を描いてみた Qiita


制御工学の問題です次の伝達関数のボード線図を折れ線近似で描け ま Yahoo 知恵袋



ボード線図 Okwave


ボード線図の書き方の基本


ボード線図



ボード線図 電験3種 理論 最速合格


宮崎技術研究所 自動制御講座 3 2 2 周波数応答による評価


第 7 週目 周波数伝達関数とボード線図 周波数伝達関数 ボード線図 Tut System Control Laboratory 1 Ppt Download



0 件のコメント:
コメントを投稿